Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Initialising ...
Fletcher, J. K.
PNC TN9410 97-065, 25 Pages, 1997/07
位置r、単位方向ベクトル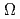 の中性子束を
の中性子束を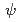 (r,
(r, 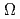 )と定義すると、多群輸送方程式は次式で表される。ただし、
)と定義すると、多群輸送方程式は次式で表される。ただし、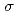 t(r)、はそれぞれ、全断面積、方向
t(r)、はそれぞれ、全断面積、方向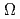 1 から
1 から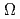 への散乱断面積、生成断面積を表し、また、
への散乱断面積、生成断面積を表し、また、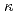 は臨界係数を、
は臨界係数を、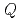 (r,
(r,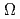 )は外部中性子源を表す。そして、この方程式を次の球面調和関数展開を用いて解く。ここで、
)は外部中性子源を表す。そして、この方程式を次の球面調和関数展開を用いて解く。ここで、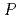
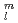 (cos
(cos 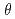 )はオーダー
)はオーダー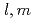 のルジャンドル陪関数で、
のルジャンドル陪関数で、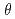 と
と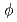 はそれぞれ方向
はそれぞれ方向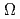 の仰角及び方位角を表す。NはPN近似の次数を表す。三角関数の多項式である球面調和関数の直交性と漸化式を用いることにより、展開係数とに関する1階の微分方程式が導かれる。
の仰角及び方位角を表す。NはPN近似の次数を表す。三角関数の多項式である球面調和関数の直交性と漸化式を用いることにより、展開係数とに関する1階の微分方程式が導かれる。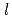 が奇数の項を消去することにより、拡散方程式の場合に用いられるような通常の有限差分法により解くことの可能な、2次の微分方程式が導かれる。メッシュ誤差低減は、その記述式の高次の差分項を保持したまま、2次式を用いて数値的に近似することにより行われる。当手法の採用により、メッシュ誤差は大幅に減少され、他の手法、特にモンテカルロ法により得られたものに匹敵する結果を直接計算することが可能となった。
が奇数の項を消去することにより、拡散方程式の場合に用いられるような通常の有限差分法により解くことの可能な、2次の微分方程式が導かれる。メッシュ誤差低減は、その記述式の高次の差分項を保持したまま、2次式を用いて数値的に近似することにより行われる。当手法の採用により、メッシュ誤差は大幅に減少され、他の手法、特にモンテカルロ法により得られたものに匹敵する結果を直接計算することが可能となった。
熊沢 蕃
電子通信学会論文誌,A, 61(8), p.774 - 781, 1978/08
本論は、方向依存性のある器官線量を精度よく評価する上で必要とされる、少数のデータに基づく有限球面調和展開法に関する。従来、この種の展開は地球物理学上のデータ解析に用いられているが、従来の展開法による各項は必ずしも一次独立ではない。従って、少数のデータを用いて一次連立方程式により展開係数を一義的に求めることができない。本論では、実験データの取り易い「球面格子点」を天頂角、方位角をそれぞれ等分した交点のセットと定義し、このセットに関して一次独立な球面調和関数を誘導することにより、その展開形を明らかにした。この他のセットについても検討を行っている。あらゆる内挿点で同じ値をもたらす球面格子点に関する球面調和展開と2次元フーリェ展開の関係も検討されている。本展開法は従来のものより高い次数の項を含む特徴がある。本展開法により器官線量データの球面調和展開が可能となり、又他への適用も化膿。
熊沢 蕃
電子通信学会論文誌,A, 61-A(10), p.1053 - 1054, 1978/00
本稿は、球座標系での等間隔標本点データから離散型球面調和展開係数を求めるのに、調和成分の選点直交性を考慮する方法について述べてある。天頂角(0~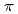 )をN
)をN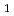 等分、方位角(0~2
等分、方位角(0~2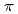 )をN
)をN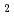 等分し、標本点
等分し、標本点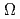 st=(
st=(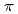 s/N
s/N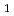 ,2
,2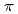 t/N
t/N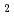 )、(s=1,…,N
)、(s=1,…,N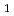 -1,t=0,…,N
-1,t=0,…,N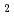 -1)とすると、標本点の総数N
-1)とすると、標本点の総数N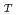 =(N
=(N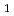 -1)N
-1)N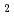 である。従って、N
である。従って、N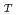 次の連立一次方程式からN
次の連立一次方程式からN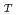 個の展開係数が求められる。然るに、離散型球面調和関数をフーリエとルジャンドル成分に分解して、これらの調和関数に部分的な選点直交性のあることを示すことができる。これにより、N
個の展開係数が求められる。然るに、離散型球面調和関数をフーリエとルジャンドル成分に分解して、これらの調和関数に部分的な選点直交性のあることを示すことができる。これにより、N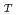 個の展開係数は、2N
個の展開係数は、2N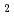 個の高々〔N
個の高々〔N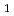 /2〕次の連立一次方程式を解くことにより求められることが示される。本稿は器官線量や検出器の方向依存性を球面調和展開するにあたり、従来必ずしも明らかではなかった標本点データに基づく解析法を明らかにする取り組みの一つである。この展開法を用いることにより、器官線量や検出器の方向依存性を簡単に評価することができる。
/2〕次の連立一次方程式を解くことにより求められることが示される。本稿は器官線量や検出器の方向依存性を球面調和展開するにあたり、従来必ずしも明らかではなかった標本点データに基づく解析法を明らかにする取り組みの一つである。この展開法を用いることにより、器官線量や検出器の方向依存性を簡単に評価することができる。